이진 탐색 트리 (Binary Search Tree, BST)

각 노드가 최대 두 개의 자식 노드를 가지며, 각 노드의 왼쪽 서브 트리는 해당 노드보다 작은 값들로, 오른쪽 서브 트리는 해당 노드보다 큰 값들로 이루어진 자료구조이다.
이렇게 구성된 트리는 탐색 및 삽입 연산이 빠르게 수행된다.

🔗 Binary Tree 3가지 순회방법
🔗 BST insertion/deletion

이진 탐색 트리 특징

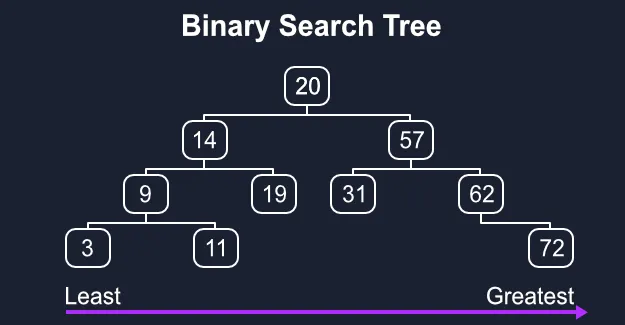
• 정렬된 구조: 모든 노드는 왼쪽 자식 < 부모 < 오른쪽 자식 규칙을 따른다.
  이 덕분에 데이터가 자연스럽게 정렬된 상태를 유지한다.
• 범위 시각화: 이미지 하단의 화살표처럼, 가장 왼쪽에 있는 노드가 최솟값(Least), 가장 오른쪽에 있는 노드가 최댓값(Greatest)이 된다.
• 효율적인 탐색: 균형이 잘 잡힌 트리의 경우, 모든 연산(탐색, 삽입, 삭제)의 시간 복잡도는 트리의 높이에 비례하는 O(log n)이다.

시간 복잡도

연산	평균	최악 (편향 트리)
탐색 (Search)	O(log n)	O(n)
삽입 (Insert)	O(log n)	O(n)
삭제 (Delete)	O(log n)	O(n)

트리가 한쪽으로 치우친 편향 트리(Skewed Tree)가 되면 연결 리스트와 다를 바 없어 O(n)이 된다.
이를 방지하기 위해 AVL 트리, Red-Black 트리 등 균형 트리를 사용한다.

주요 연산

탐색 (Search)

루트에서 시작하여, 찾고자 하는 값이 현재 노드보다 작으면 왼쪽, 크면 오른쪽으로 이동한다.

function search(node, target) {
  if (target === node.value) {
    return node;
  } else if (target < node.value) {
    return search(node.left, target);
  } else {
    return search(node.right, target);
  }
}

삽입 (Insert)

탐색과 동일한 방식으로 내려가다가, 빈 자리(null)를 만나면 새 노드를 삽입한다.

function insert(node, value) {
  if (node === null) {
    return new Node(value);
  }

  if (value < node.value) {
    node.left = insert(node.left, value);
  } else if (value > node.value) {
    node.right = insert(node.right, value);
  }

  // 중복 값은 무시
  return node;
}

삭제 (Delete)

삭제는 3가지 케이스로 나뉜다.

1. 자식이 없는 노드: 그냥 삭제
2. 자식이 하나인 노드: 자식을 현재 위치로 올림
3. 자식이 둘인 노드: 오른쪽 서브트리의 최솟값(또는 왼쪽 서브트리의 최댓값)으로 대체

function deleteNode(node, target) {
  if (node === null) return null;

  if (target < node.value) {
    node.left = deleteNode(node.left, target);
  } else if (target > node.value) {
    node.right = deleteNode(node.right, target);
  } else {
    // 삭제할 노드를 찾음

    // Case 1 & 2: 자식이 없거나 하나인 경우
    if (node.left === null) return node.right;
    if (node.right === null) return node.left;

    // Case 3: 자식이 둘인 경우
    // 오른쪽 서브트리에서 최솟값을 찾아 대체
    let minNode = node.right;
    while (minNode.left !== null) {
      minNode = minNode.left;
    }
    node.value = minNode.value;
    node.right = deleteNode(node.right, minNode.value);
  }

  return node;
}

자바스크립트로 BST 구현하기

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  // 삽입
  insert(value) {
    const newNode = new Node(value);

    if (this.root === null) {
      this.root = newNode;
      return this;
    }

    let current = this.root;
    while (true) {
      if (value === current.value) return this; // 중복 무시

      if (value < current.value) {
        if (current.left === null) {
          current.left = newNode;
          return this;
        }
        current = current.left;
      } else {
        if (current.right === null) {
          current.right = newNode;
          return this;
        }
        current = current.right;
      }
    }
  }

  // 탐색
  search(value) {
    let current = this.root;

    while (current !== null) {
      if (value === current.value) return current;
      if (value < current.value) {
        current = current.left;
      } else {
        current = current.right;
      }
    }

    return null;
  }

  // 중위 순회 (정렬된 순서로 출력)
  inOrderTraversal(node = this.root, result = []) {
    if (node !== null) {
      this.inOrderTraversal(node.left, result);
      result.push(node.value);
      this.inOrderTraversal(node.right, result);
    }
    return result;
  }

  // 최솟값
  findMin(node = this.root) {
    while (node.left !== null) {
      node = node.left;
    }
    return node.value;
  }

  // 최댓값
  findMax(node = this.root) {
    while (node.right !== null) {
      node = node.right;
    }
    return node.value;
  }
}

const bst = new BinarySearchTree();
bst.insert(10);
bst.insert(5);
bst.insert(15);
bst.insert(3);
bst.insert(7);

console.log(bst.inOrderTraversal()); // [3, 5, 7, 10, 15]
console.log(bst.search(7)); // Node { value: 7, ... }
console.log(bst.findMin()); // 3
console.log(bst.findMax()); // 15